Hidden Markov Model (HMM) Tagger in Natural Language Processing

Hidden Markov Model (HMM) Tagger is a Stochastic POS Tagger. It is a probabilistic sequence model; i.e. given possible sequences of tags, a HMM Tagger will compute and assign the best sequence.

To read about POS Tagging, refer to our previous blog Part Of Speech Tagging – POS Tagging in NLP.

Hidden Markov Model – HMM

A Hidden Markov Model is a Markov Process with Hidden or Unobserved states. It assumes that given a hidden state, the next state depends on the current hidden state along with other observation states.

For example, consider the diagram below. Here, Rainy and Sunny are hidden states that depend on observed states of Walk, Shop or Clean.

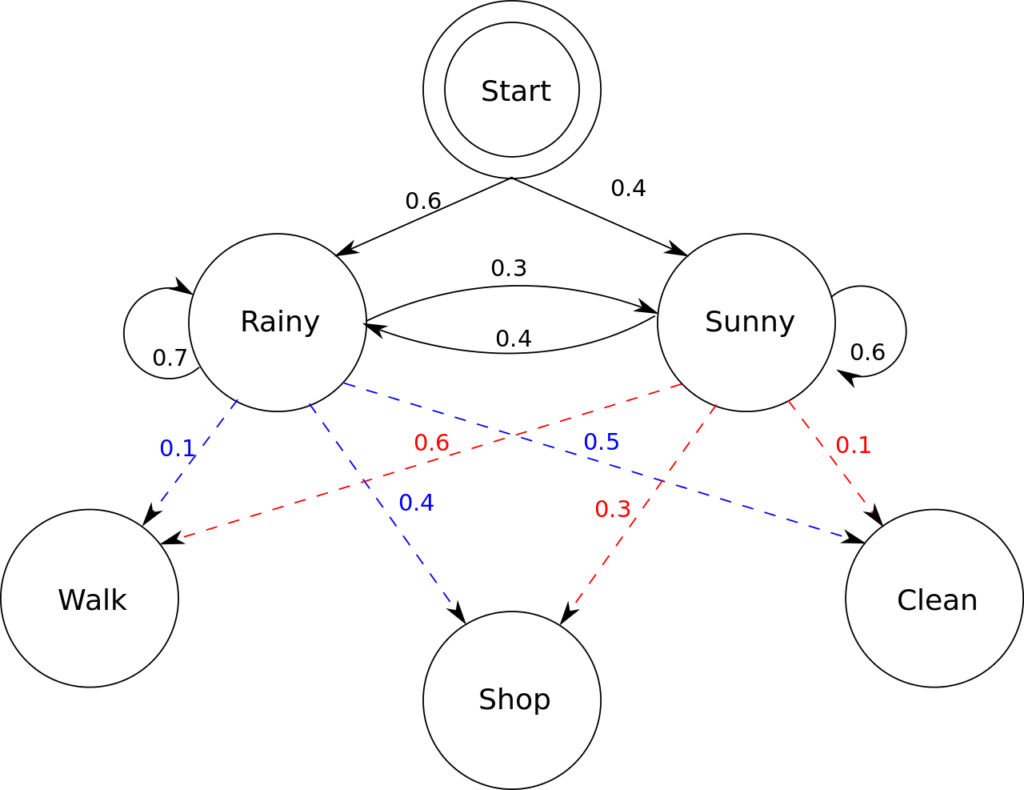
For a Hidden Markov Model in the domain of NLP, we have the following values:

1. States: Hidden States – POS Tags; i.e. VP, NP, JJ, DT
2. Emission Probability: P(w_i | t_i) – Probability that given a tag t_i, the word is w_i; e.g. P(book| NP) is the probability that the word book is a Noun.
3. Transition Probability Matrix: P(t_i+1| t_i) – Transition Probabilities from one tag t_i to another t_i+1; e.g. P(VP | NP) is the probability that current tag is Verb given previous tag is a Noun.
4. Observation: Words
5. Initial Probability: Probability of the initial word

Viterbi Decoding

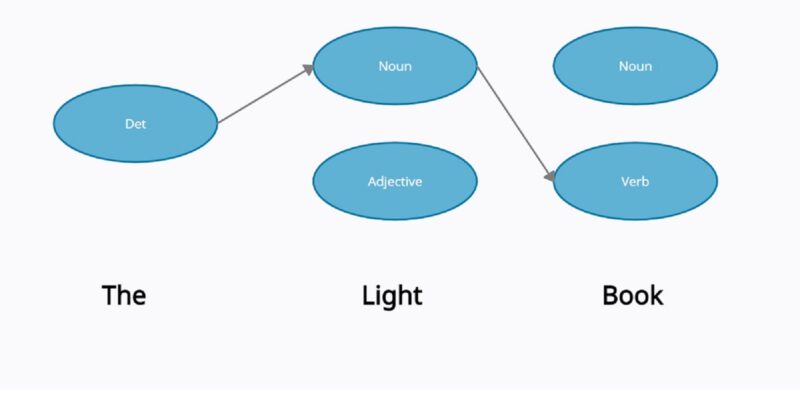
Following the above information, let’s consider a phrase “The Light Book” and try to find the best sequence label.

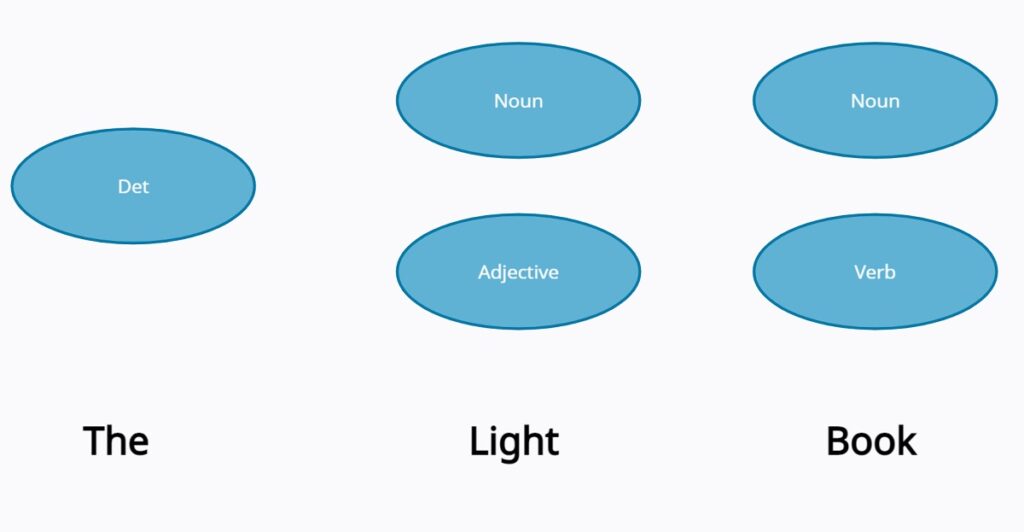
1. States: Noun, Det (determiner), Verb, Adj (Adjective)
2. Emission Probabilities:

P(word | tag)	Noun	Det	Verb	Adj
The	–	1	–	–
Light	0.03	–	–	0.02
Book	0.03	–	0.03	–

3. Transition Probabilities:

P(ti+1 | ti)	Noun	Det	Verb	Adj
Noun	0.2	0.5	0.2	0.4
Det	–	–	–	–
Verb	0.3	0.001	0.1	0.001
Adj	0.1	0.4	–	–

4. Observations: All words in the sentence, i.e. the, light and book
5. Initial Probability: Assume P(“the” | <S>) = 1

Note: These are dummy values, however, in a real scenario, these values are generated using huge corpus of data.

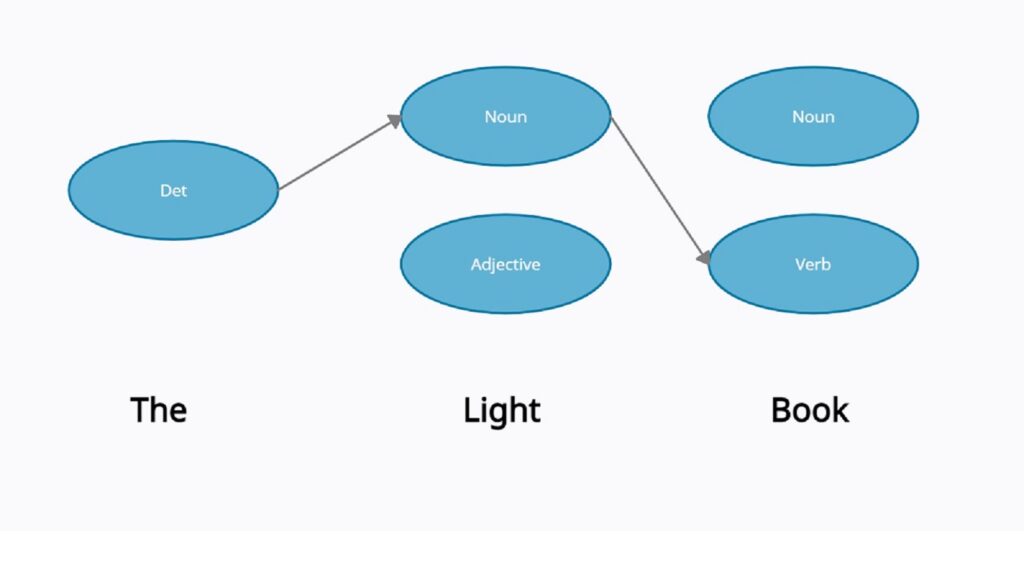
Now that we have the required values, we can find the best sequence for the given phrase.

Assigning the best sequence

Since P(“the”|<s>) = 1, we have only one word to start with: “the“. Following first word as “the”, we now find the best tag for it.

From the table, the can only possible tag is Det P(“the” | Det) = 0.3, hence, we assign “Det” to our first word; i.e. “The” is a “Det“.

Now that we know our first word, we calculate the probabilities for further sentences. However, the word “light” has more than one possible tag. Therefore, we will find probabilities for both possible tags.

P("the light") -> light is "Noun" =  P("the" | <S>) . P("the" | "Det") . P("light" | Noun) . P(Noun | Det)
                                 = 1 * 1 * 0.03 * 0.5 = 0.015
P("the light") -> light is "Adj" = P("the" | <S>) . P("the" | "Det") . P("light" | Adj) . P(Adj | Det)
                                 = 1 * 1 * 0.02 * 0.4 = 0.008

Similarly, we find the probabilities for all the possible sentences (4 combinations):

1. the -> Det; light -> Noun; book -> Noun = 0.00009
2. the -> Det; light -> Noun; book -> Verb = 0.000135
3. the -> Det; light -> Adj; book -> Noun = 0.000096
4. the -> Det; light -> Adj; book -> Verb = 0.0000024

Since the lowest sequence probability is for the -> Det + light -> Noun +book -> Verb, we can say that it has the highest likelihood for the correct probability. Thus, for this phrase, the assigned sequence will be:

The[Det] light[Noun] book[Verb]

Further in series: WordNet in Natural Language Processing

References

• Hidden Markov model – Wikipedia
• Part Of Speech Tagging – POS Tagging in NLP